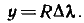|  |
тел.: +7 495 1087345 факс.: +7 495 1087345 office@trans-service.org |
Навигация
Нормальная равноугольная цилиндрическая проекция меркатора
Рассмотрим, при каком условии обеспечивается равноугольность меркаторской проекции. Для этого, принимая Землю за шар радиусом R, возьмем на ней элементарно малый отрезок локсодромии АВ. Через начальную и конечную точки проведем меридианы РNАL1 и PNBL2, а через точку В — отрезок параллели СВ (см. рис. 30,а).
В результате построения получили элементарно малый сферический треугольник ABC, который можно принять за плоский и прямоугольный.
В этом треугольнике угол РNАВ определяет направление локсодромии, т.е. курс судна К для перехода из точки А в точку В.
Рассуждая аналогично, как и при выводе уравнения локсодромии, можем написать
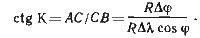
Спроектируем участок земной поверхности, ограниченный меридианами РNАL1 и PNBL2, на плоскость. Меридианы изобразятся в виде двух параллельных прямых, перпендикулярных проекциям отрезков экватора и параллели (рис. 30, б). В полученном на плоскости треугольнике abc катет cb будет равен длине отрезка экватора l1l2, т.е. cb = l1l2 = RΔλ. Катет ас обозначим ΔD, а угол cab — K1.
Из треугольника авс имеем
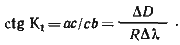
Так как мы хотим определить условие равноугольности меркаторской проекции, то примем, что углы на местности и на проекции равны К=K1
Следовательно: ctgK = ctgK1 и
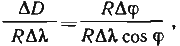
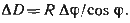
Перейдем от элементарно малых приращений к бесконечно малым
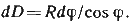
Проинтегрируем выражение от 0 до φ, получим
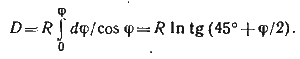 (59)
(59)
Величина D представляет собой расстояние по меридиану от экватора до заданной параллели в меркаторской проекции и называется меридиональной частью (МЧ).
Таким образом, только потому, что каждая параллель, вытянутая до длины экватора, отстоит от него на соответствующее ей расстояние D, проекция Меркатора равноугольна.
Меридиональная часть — величина линейная и, с точки зрения картографии, ее удобнее выражать в экваториальных милях, т.е. через длину 1' дуги экватора.
1 экв. миля = R arc 1' =R/3437,7468.
Отсюда R = 3437,7468 экв. мили.
Подставим в найденное выражение D значение R в экваториальных милях, а также введем в формулу модуль т = 0,4342945 для перехода от натуральных к десятичным логарифмам:
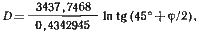
окончательно имеем D = 7 915,705' lg tg (45° + φ/2).
Однако в картографии форма Земли принимается за эллипсоид. Поэтому при составлении таблицы 26 МТ — 75 использована формула меридиональной части, в которую введен дополнительный член, учитывающий сжатие Земли. По аргументу широты, которая дана с интервалом в одну минуту, можно выбрать из этой таблицы значение меридиональной части с точностью до одной десятой экваториальной мили.
Анализ формулы (59) показывает, что при φ = 90°
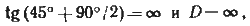
т.е. построить карту в меркаторской проекции для районов, охватывающих полюса, невозможно. Кроме того, для высоких широт проекция дает большое искажение площадей.
По этим двум причинам проекция Меркатора используется для построения морских карт только до параллели 85°.
Расстояние по меридиану между двумя параллелями на меркаторской карте, выраженное в экваториальных милях, называется разностью меридиональных частей и обозначается AD или РМЧ.
Для доказательства того, что локсодромия на меркаторской проекции изображается прямой линией из треугольника abc (см. рис. 30, б), напишем RAX/AD = tgK1 или с учетом К = К1
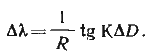
Переходя к бесконечно малым приращениям и интегрируя выражение от λ1 до λ2, будем иметь
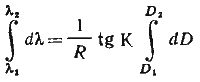
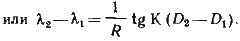
Подставив в полученное равенство значения D1 и D2, получим выражение
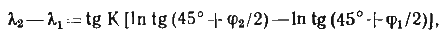
которое является уравнением локсодромии.
Отсюда можно сделать вывод, что локсодромия в проекции Меркатора действительно изображается прямой линией (в нашем примере — прямая ab). Таким образом, мы доказали, что карта в меркаторской проекции удовлетворяет ранее рассмотренным нами требованиям.
На основании общего уравнения цилиндрических проекций (57) уравнение для проекции Меркатора можно представить в следующем виде: